당신은 주제를 찾고 있습니까 “maximum likelihood estimation 설명 – 최대우도법(Maximum Likelihood Estimation) 소개“? 다음 카테고리의 웹사이트 https://dienbienfriendlytrip.com 에서 귀하의 모든 질문에 답변해 드립니다: https://dienbienfriendlytrip.com/finance/. 바로 아래에서 답을 찾을 수 있습니다. 작성자 공돌이의 수학정리노트 이(가) 작성한 기사에는 조회수 21,129회 및 415409 Like 개의 좋아요가 있습니다.
데이터의 밀도를 추정하는 한 방법으로 파라미터로 구성된 어떤 확률 밀도 함수 (x|셰타)에서 관측된 표본 데이터 집합이 있고, 이 표본에서 파라미터(셰타)를 추정하는 방법이다.
maximum likelihood estimation 설명 주제에 대한 동영상 보기
여기에서 이 주제에 대한 비디오를 시청하십시오. 주의 깊게 살펴보고 읽고 있는 내용에 대한 피드백을 제공하세요!
d여기에서 최대우도법(Maximum Likelihood Estimation) 소개 – maximum likelihood estimation 설명 주제에 대한 세부정보를 참조하세요
글로 정리된 곳: https://angeloyeo.github.io/2020/07/17/MLE.html
—
커피 한 잔의 후원이 큰 힘이 됩니다.
후원하기(카카오페이): https://qr.kakaopay.com/281006011000018389112430
후원하기(송금)
– 카카오뱅크 3333-15-3394161 (여동훈)
– 우리은행 1002-036-488593 (여동훈)
—
영상에서 사용된 모든 MATLAB 코드는 아래의 github repo에서 받아가실 수 있습니다.
https://github.com/angeloyeo/gongdols
maximum likelihood estimation 설명 주제에 대한 자세한 내용은 여기를 참조하세요.
최대우도법(MLE) – 공돌이의 수학정리노트
최대우도법(Maximum Likelihood Estimation, 이하 MLE)은 모수적인 데이터 밀도 추정 방법으로써 파라미터 으로 구성된 어떤 확률밀도함수 에서 관측 …
Source: angeloyeo.github.io
Date Published: 10/9/2022
View: 9015
Maximum Likelihood란? (MLE란?) – 유니의 프로세스마이닝 공부
두 개의 분포 · likelihood의 표현식. · 데이터 x_n이 θ=( μ, σ)의 parameter를 가지는 정규분포를 따를 확률 · likelihood 계산식 · log likelihood · 위 식을 …
Source: process-mining.tistory.com
Date Published: 3/1/2022
View: 9638
Likelihood, Maximum likelihood estimation 이란? – simpling
직관적으로 생각했을 때 후보가 되는 분포가 데이터를 잘 설명한다면 likelihood는 당연히 높게 나올 것이다. 데이터가 주어졌을 때 여러가지 후보 분포.
Source: simpling.tistory.com
Date Published: 5/18/2021
View: 8823
9.2 최대가능도 추정법 – 데이터 사이언스 스쿨
최대가능도 추정법(Maximum Likelihood Estimation, MLE)은 주어진 표본에 대해 가능도를 가장 크게 하는 모수 θ를 찾는 방법이다. 이 방법으로 찾은 모수는 기호로 …
Source: datascienceschool.net
Date Published: 1/30/2022
View: 4153
Likelihood (‘가능도’ 혹은 ‘우도’)와 MLE (Maximum Likelihood …
… 는 likelihood를 maximum할 수 있는 estimation … MLE : 주어진 데이터를 제일 잘 설명하는 모델 …
Source: aigong.tistory.com
Date Published: 12/11/2021
View: 2024
최대가능도 방법 – 위키백과, 우리 모두의 백과사전
최대가능도방법 (最大可能度方法, 영어: maximum likelihood method) 또는 최대우도법(最大尤度法)은 어떤 확률변수에서 표집한 값들을 토대로 그 확률변수의 모수를 …
Source: ko.wikipedia.org
Date Published: 10/13/2022
View: 757
Maximum Likelihood Estimation의 이해
최대가능도추정, Maximum Likelihood Estimation 혹은 최대우도법이라고 … 앞서 설명했던 샘플링 데이터 x_1, x_2, …, x_n에 대해 평균과 분산을 …
Source: synapticlab.co.kr
Date Published: 6/24/2022
View: 2905
주제와 관련된 이미지 maximum likelihood estimation 설명
주제와 관련된 더 많은 사진을 참조하십시오 최대우도법(Maximum Likelihood Estimation) 소개. 댓글에서 더 많은 관련 이미지를 보거나 필요한 경우 더 많은 관련 기사를 볼 수 있습니다.
주제에 대한 기사 평가 maximum likelihood estimation 설명
- Author: 공돌이의 수학정리노트
- Views: 조회수 21,129회
- Likes: 415409 Like
- Date Published: 2020. 7. 23.
- Video Url link: https://www.youtube.com/watch?v=XhlfVtGb19c
MLE(Maximum Likelihood Estimation) 최대우도법
최대 우도법이 잘 이해가 가지 않는다면 유투브 StatQuest with Josh Starmer의 위 동영상을 봅시다
정말 간결하고 이해가 잘되서 갖고 와봤습니다 ~.~
최대우도법은 단어 그대로 ‘우도(likelihood, 가능도)’를 ‘최대화’하는 지점을 찾는 것을 의미합니다.
우도(Likelihood)
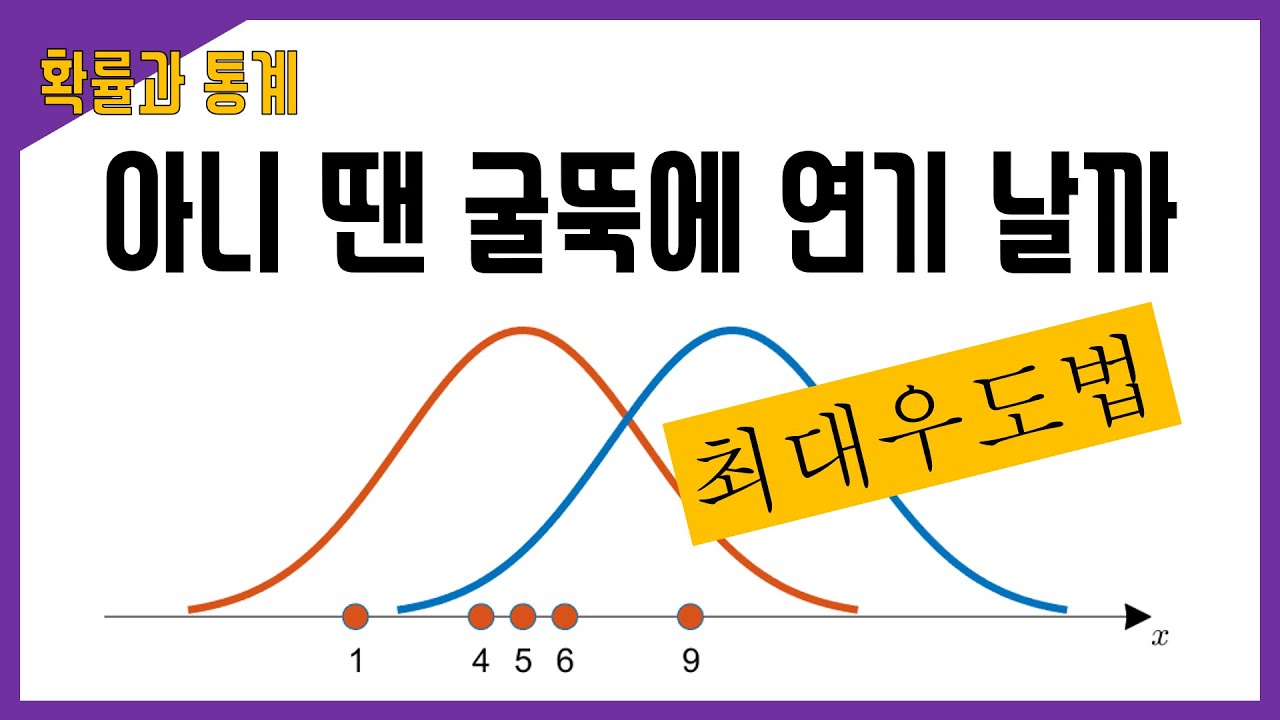
x={1,4,5,6,9}인 데이터로 추정되는 분포 주황색, 파란색 중 어느 곡선으로부터 추출되었을 확률이 더 높을까? 출처-공돌이의 수학노트
“데이터가 이 분포로부터 나왔을 가능도”
우리가 가지고 있는 데이터는 보통 모집단(population)에서 일부분(sample)을 가져왔을 것이다.
예를 들어서 모델링하고자 하는 문제가 “남반구 지역의 물고기 개체수를 예측”하는 것이라고 해보자, 그렇다면 풀고자 하는 문제의 모집단은 “남반구 지역의 시간에 따른 전체 물고기 개체수”지만 관측된 데이터는 모든 물고기 수는 아닐 것이다. 그렇다면 전체 물고기 수의 분포와 관측으로 얻어진 물고기 수의 분포가 약간 다를 수 있다. 하지만 가지고 있는 관측 데이터에 맞춰진 분포를 우도라고 한다.
결국 우도가 가지는 의의는 “모델과 추정치의 우도가 높으면 좋다.”라는 것이다. 즉 모델과 추정치가 데이터와 잘 맞으면, 데이터를 잘 설명하는 높아지는 값이며 “모델과 추정치가 데이터와 잘 맞는 정도를 확률로 표현한 것”을 의미한다.
확률(Probability) vs 우도(Likelihood)
확률은 P(data|distribution) 분포가 주어졌을데 데이터의 확률을 의미하며,(분포는 고정)
우도는 L(distribution|data) 데이터가 주어졌을 때 분포의 likehood를 의미한다.(데이터는 고정)
즉, 확률은 원인이 모델과 추정치이고 결과가 확률일 때 사용한다.
ex. 평균이 4이고 표준편차가 0.5일 때 5일 확률은?
그리고 우도는 원인이 데이터이고 결과가 모델, 추정치일 때 사용한다.
ex. 동전을 3번 던져 모두 앞면이 나올 확률은?
MLE(Maximum Likelihood Estimation) 최대우도법
데이터의 밀도를 추정하는 한 방법으로 파라미터로 구성된 어떤 확률 밀도 함수 (x|셰타)에서 관측된 표본 데이터 집합이 있고, 이 표본에서 파라미터(셰타)를 추정하는 방법이다.
표본 데이터(sample)를 모두 평균 값으로 지정해 likelihood 값을 계산하고 likelihood가 가장 큰 지점을 찾는다. 이렇게 찾게된 지점은 데이터와 제일 잘 맞는 모델과 추정치를 계산할 수 있게 된다.
모델 파라미터를 관측 값에만 의존하여 예측하는 방법으로 주어진 파라미터를 기반으로 likelihood를 최대화 한다.
likelihood function log-likelihood function
likelihood function의 최대값을 찾는 방법을 MLE라고 한다. 계산의 편의를 위해 log-likelihood function의 최대값을 찾으며 최대값을 찾을 때 ‘미분계수’를 이용한다. 셰타에 대해 편미분하고 그 값이 0이 되도록하는 셰타를 찾는 과정을 통해 L(셰타|x)를 최대화 하는 셰타를 찾으면 된다.
log-likelihood function의 편미분
MLE 특징
Asymptotically optimal
최소한 consistent한 다른 추정값과 비교했을 때 MLE는 가장 작은 variance를 가진다.
ex. 평균의 MLE는 sample mean인데 sample mean의 variance가 sample median의 variance보다 작다.
n이 무한대로 갈 때 표준정규분포를 따른다.
Equivalent
Unbiased가 아니지만 consistent하다.
※ MAP(Maximum a Posteriori Estimiation) 최대 사후 확률 추정법
주어진 관측 결과와 사전 확률을 결합해 최적의 모수를 찾아내는 방법
MLE가 f(X|셰타)라면 MAP는 f(셰타|X)이다.
데이터와 제일 잘 맞는 추정치를 찾고 주어진 데이터를 기반으로 최대 확률을 갖는 파라미터를 찾는다. MLE의 리스크를 해결
딥러닝이랑 결국 데이터의 분포에 모델 파라미터를 근사시키는 과정이다. MLE, MAP, 베이지안(MLE와 MAP는 베이지안의 근간)모두 이 아이디어에서 근거한 개념이기 때문에 MLE는 딥러닝을 하려면 꼭 알아야 하는 개념 중 하나라고 할 수 있다.
References
https://angeloyeo.github.io/2020/07/17/MLE.html
https://rpubs.com/Statdoc/204928
공돌이의 수학정리노트
어떤 평균값을 갖는 확률밀도로 부터 이 샘플들이 추출되었을까?
adapted from the Seeing Theory’s amazing visualization of MLE
최대우도법의 정의
최대우도법(Maximum Likelihood Estimation, 이하 MLE)은 모수적인 데이터 밀도 추정 방법으로써 파라미터 으로 구성된 어떤 확률밀도함수 에서 관측된 표본 데이터 집합을 이라 할 때, 이 표본들에서 파라미터 를 추정하는 방법이다.
당연히, 이 말만 보면 MLE가 뭔지 이해하기는 불가능하기 때문에 예시를 들어 MLE에 대해 알아보도록 하자.
MLE의 toy example 예시
MLE의 핵심 아이디어를 이해하기 위해 아래와 같은 매우 간단한 toy example을 생각해보자.
다음과 같이 5개의 데이터를 얻었다고 가정하자.
이 때, 아래의 그림을 봤을 때 데이터 는 주황색 곡선과 파란색 곡선 중 어떤 곡선으로부터 추출되었을 확률이 더 높을까?
그림 1. 획득한 데이터와 추정되는 후보 분포 2개(각각 주황색, 파란색 곡선으로 표시)
눈으로 보기에도 파란색 곡선 보다는 주황색 곡선에서 이 데이터들을 얻었을 가능성이 더 커보인다.
왜냐면 획득한 데이터들의 분포가 주황색 곡선의 중심에 더 일치하는 것 처럼 보이기 때문이다.
이 예시를 보면, 우리가 데이터를 관찰함으로써 이 데이터가 추출되었을 것으로 생각되는 분포의 특성을 추정할 수 있음을 알 수 있다. 여기서는 추출된 분포가 정규분포라고 가정했고, 우리는 분포의 특성 중 평균을 추정하려고 했다.
그럼 좀 더 구체적으로, 수학적인 방법으로 정밀하게 이 분포의 특성을 추정하는 방법을 이해해보도록 하자.
Likelihood function
앞서 언급한 수학적인 추정방법을 언급하기 위해 데이터의 likelihood 기여도에 대해 얘기해보자.
그림 2. 주황색 후보 분포에 대해 각 데이터들의 likelihood 기여도를 점선의 높이로 나타냈다.
likelihood 라는 것은 특별히 어려운 것이 아니고, 지금 얻은 데이터가 이 분포로부터 나왔을 가능도를 말한다.
수치적으로 이 가능도를 계산하기 위해서는 각 데이터 샘플에서 후보 분포에 대한 높이(즉, likelihood 기여도)를 계산해서 다 곱한 것을 이용할 수 있을 것이다.
계산된 높이를 더해주지 않고 곱해주는 것은 모든 데이터들의 추출이 독립적으로 연달아 일어나는 사건이기 때문이다.
그렇게 해서 계산된 가능도를 생각해볼 수 있는 모든 후보군에 대해 계산하고 이것을 비교하면 우리는 지금 얻은 데이터를 가장 잘 설명할 수 있는 확률분포를 얻어낼 수 있게 된다.
지금까지 얘기한 likelihood를 조금 더 수학적으로 서술하면 다음과 같이 쓸 수 있다.
아래와 같이 전체 표본집합의 결합확률밀도 함수를 likelihood function이라고 한다.
위 식의 결과 값이 가장 커지는 를 추정값 로 보는 것이 가장 그럴듯하다.
위 식을 likelihood function이라고 하고 보통은 자연로그를 이용해 아래와 같이 log-likelihood function 를 이용한다.
Likelihood function의 최대값을 찾는 방법
결국 Maximum Likelihood Estimation은 Likelihood 함수의 최대값을 찾는 방법이라 할 수 있다.
log 함수는 단조증가 함수이기 때문에 likelihood function의 최대값을 찾으나 log-likelihood function의 최대값을 찾으나 두 경우 모두의 최대값을 갖게 해주는 정의역의 함수 입력값은 동일하다.
따라서, 보통은 계산의 편의를 위해 log-likelihood의 최대값을 찾는다.
어떤 함수의 최대값을 찾는 방법 중 가장 보편적인 방법은 미분계수를 이용하는 것이다.
즉, 찾고자하는 파라미터 에 대하여 다음과 같이 편미분하고 그 값이 0이 되도록 하는 를 찾는 과정을 통해 likelihood 함수를 최대화 시켜줄 수 있는 를 찾을 수 있다.
MLE의 좀 더 복잡한 예시 (모평균, 모분산 추정)
평균 와 분산 를 모르는 정규분포에서 표본 을 추출했을 때, 이들 값을 이용해서 모분포의 평균과 분산을 추정해보자. 익히 들어서 알겠지만 표본을 위와 같이 추출하였다고 하면 모평균의 추정값은
이고 모분산의 추정값은
이다. 이것을 최대우도법을 이용해서 확인해보도록 하자.
각각의 표본들은 정규분포에서 추출된다고 했을 때 각 표본의 표본분포는
이고, 은 모두 독립적으로 추출했다고 가정하자. 그러면 우도(likelihood)는
이고, 로그-우도는
이다. 따라서 를 에 대해 편미분하면,
따라서 최대우도를 만들어주는 모평균의 추정량은
이다.
한편, 를 표준편차 로 편미분하면
따라서, 최대우도를 만들어주는 모분산의 추정량은
이라는 것을 알 수 있다.
참고 문헌
Maximum Likelihood란? (MLE란?)
이번 포스팅에서는 Maximum Likelihood가 무엇인지에 대해 알아보겠다. 이 포스팅은 정규 분포에 대한 이해가 있다고 가정한다.
Likekihood
Likelihood란, 데이터가 특정 분포로부터 만들어졌을(generate) 확률을 말한다. 예를 들어, X = (1, 1, 1, 1, 1)이라는 데이터가 있다고 하자. 그리고 아래와 같이 두 분포가 있다고 하자.
두 개의 분포
우리의 데이터 X는 어떤 분포를 따를 확률이 더 높을까? 당연히 왼쪽 분포를 따를 확률이 더 높을 것이다. 이런 상황에서 우리는 왼쪽 분포의 데이터 X에 대한 likelihood가 더 높다고 표현할 수 있다. 그러므로 likelihood는 다음과 같은 식으로 표현할 수 있다.
likelihood의 표현식. θ의 parameter를 가지는 분포.
그렇다면 이 likelihood는 어떻게 계산할 수 있을까? 우리의 distribution(분포)이 θ=(μ, σ) 의 parameter를 가지고 있는 정규분포라고 가정하자. 그러면 한 개의 데이터가 이 정규분포를 따를 확률은 다음과 같이 계산할 수 있을 것이다. (그냥 정규 분포의 PDF에 x_n 값을 넣은 것이다.)
데이터 x_n이 θ=( μ, σ)의 parameter를 가지는 정규분포를 따를 확률
그렇다면 모든 데이터들이 독립적(independent)이라고 가정하면 다음과 같은 likelihood 식을 얻을 수 있다.
likelihood 계산식
Maximum Likelihood
log likelihood
우리는 위 설명에서 likelihood의 계산식을 얻었다. 데이터 X가 θ의 parameter를 가지는 distribution을 따르려면 이 likelihood가 최대가 되는 distribution을 찾아야 할 것이다. 우리는 최댓값을 구할 때 주로 미분을 사용한다. 하지만 식이 곱셈(pi)으로 연결되어 있는 탓에 이 식에 바로 미분을 적용하기는 쉽지 않다. 그러므로 우리는 이 식에 log와 -를 취해서 그 값이 최소가 되는 값을 구함으로써 maximum likelihood를 만들어주는 값을 구한다. 이 식을 log likelihood라고 한다.
log likelihood
Maximum Likelihood의 계산
그러면 이제 likelihood를 최대화하는 (log likelihood를 최소화하는) θ 값을 찾을 차례이다. 이를 위해 우리는 log likelihood 식을 미분하고, 이 식이 0이 되는 값(극솟값)을 찾는다. 즉, 다음 식을 만족하는 θ 값을 찾아야 하는 것이다.
위 식을 만족하는 θ 값을 찾아야 한다. 뒤 식이 저 형태인 이유는 ln(f(x))를 x에 대해 미분하면 f'(x)/f(x) 형태가 되기 때문이다.
저 θ 값을 찾으면 우리는 likelihood를 최대화할 수 있다. 이의 계산 과정을 보이기 위해 정규 분포를 예로 들어서 설명하도록 하겠다. 우리의 분포가 θ=( μ, σ)의 정규분포라면 p 값은 다음과 같은 식일 것이다. (정규분포의 PDF이다.)
정규분포의 p 값
그러므로 우리는 이 식을 위 식에 적용시키면 다음과 같은 계산과정에 따라 최종 결과를 얻을 수 있다. (자세한 미분 계산 과정은 생략한다. 미분 과정에 대한 질문은 댓글로 가능하다.)
log likelihood를 미분하는 식.
우리는 위 식을 0으로 만드는 parameter θ=(μ, σ)을 찾아야 한다. σ는 분모에 있기 때문에 이 값으로는 식을 0으로 만들 수 없다. 그러므로 우리는 μ 값을 다음과 같이 정의함으로써 식을 0으로 만들 수 있다.
maximum likelihood mu 값
이 평균(μ) 값을 이용해 우리는 분산(σ) 값 또한 도출해낼 수 있다.
도출된 분산값
이처럼 likelihood를 최대화하는 parameter 값을 maximum likelihood estimate라고 한다. 즉, 위 평균 값과 분산 값의 parameter가 정규분포에 대한 maximum likelihood estimate인 것이다.
이번 포스팅에서는 maxium likelihood estimation이 무엇인지에 대해 알아보았다. maximum likelihood 기법은 머신러닝에서 모수를 추정할 때 가장 자주 쓰이는 개념 중에 하나이다. 하지만 maximum likelihood는 분산을 실제보다 작게 추정하여 표본에 대하여 overfitting될 수도 있다는 한계점도 지닌다.
반응형
Likelihood, Maximum likelihood estimation 이란?
딥러닝 공부를 하다 보면 likelihood가 자주 등장한다. 기본적인 내용들을 다시 한번 remind 하기 위해 정리해둔다.
Likelihood를 식으로 표현하면 다음과 같다.
$$ L(\theta|D) $$
$\theta$는 parameter이고 D는 data를 의미한다. 식을 그대로 해석해보면, 가능도는 관측값(D)이 주어졌을 때(given) 관측값이 $\theta$에 대한 확률분포 $P(\theta)$에서 나왔을 확률이다.
likelihood가 익숙하면서 안 익숙한(?) 이상한 느낌이 드는 이유는 likelihood와 비슷하게 생긴 $Pr(D|\theta)$라는 식을 자주 보았기 때문이다. 이 식은 ‘확률’을 나타내는데 중, 고등학교 과정에서 자주 봤었다. 확률은 가능도와 다르게 확률분포 $P(\theta)$가 주어졌을 때(given) Data가 이 분포에서 관측될 수 있는 빈도를 표현한다.
정규분포
예를 들어 정규 분포가 주어지고 데이터가 0~1$\sigma$ 사이로 관측될 확률은 34.1% 가 된다. 즉, 확률은 given distribution에서 데이터가 관측되게 될 범위의 area가 된다.
가능도와 확률의 차이는 명확하다. 확률은 주어진 확률분포에서 해당 관측값이 어느 정도 나올지를 표현하고 이 값은 distribution의 area를 통해 구한다. 반면 가능도는 관측 데이터가 있을 때 어떤 분포를 주고 그 분포에서 데이터가 나왔을 확률을 구하는 것이다. 가능도를 구하는 식은 다음과 같다.
$$ L(\theta|x) = P_{\theta} (X=x) = \prod^{n}_{k=1} P(x_{k}|\theta) $$
즉, 가능도는 각 데이터 샘플에서 후보 분포 $P(\theta)$에 대한 y value(밀도)를 (데이터의 추출이 독립적이고 연달아 일어나는 사건이므로) 곱하여 계산한다. 직관적으로 생각했을 때 후보가 되는 분포가 데이터를 잘 설명한다면 likelihood는 당연히 높게 나올 것이다.
데이터가 주어졌을 때 여러가지 후보 분포
예를 들어 위의 그림처럼 파란색 데이터 분포를 설명하는 후보 분포가 1,2,3으로 주어졌다고 가정해보자. 이때 각 분포에 대한 likelihood를 구하면 데이터를 잘 설명하는 2번이 가장 큰 값을 가지게 될 것이다. 이렇게 가장 데이터를 잘 설명하는 분포를 likelihood를 통해 구할 수 있고 이런 방법을 Maximum Likelihood Estimation (MLE)라고 부른다.
다시 한번 MLE를 정의해보면 다음과 같다. 관측된 표본 데이터 집합을 X라고 했을 때 parameter $\theta$로 구성된 확률 밀도 함수(pdf)에서 $\theta$를 추정하는 방법이다. 이 $\theta$는 Likelihood $L(\theta|x)$를 maximize 함으로 찾을 수 있다. 보통은 파라미터 $\theta$에 대해 편미분 하여 그 값이 0이 되도록 하는 파라미터를 찾는다.
참조 : wikipedia (likelihood)
반응형
9.2 최대가능도 추정법 — 데이터 사이언스 스쿨
모멘트 방법으로 추정한 모수는 그 숫자가 가장 가능성 높은 값이라는 이론적 보장이 없다. 이 절에서는 이론적으로 가장 가능성이 높은 모수를 찾는 방법인 최대가능도 추정법에 대해 알아본다. 최대가능도 추정법은 모든 추정방법 중 가장 널리 사용되는 방법이다. 먼저 가능도함수에 대해 알아보고 베르누이분포, 카테고리분포, 정규분포, 다변수정규분포 등 여러 기본분포의 모수를 최대가능도 추정법으로 추정하는 방법을 공부한다.
in
for
in
for
c
c
c
c
\[\begin{split} \begin{align} \begin{aligned} &\log L(\mu; x_1, x_2, x_3) \\ &= \log \left( \dfrac{1}{(2\pi\sigma^2)^{\frac{3}{2}}} \exp\left({-\frac{3\mu^2+4\mu+10}{2\sigma^2}}\right) \right) \\ &= \log \left( \dfrac{1}{(2\pi\sigma^2)^{\frac{3}{2}}} \right) -\frac{3\mu^2+4\mu+10}{2\sigma^2} \\ &= \log \left( \dfrac{1}{(2\pi\sigma^2)^{\frac{3}{2}}} \right) -\frac{3\left(\mu+\frac{2}{3}\right)^2+\frac{26}{3}}{2\sigma^2} \\ \end{aligned} \tag{9.2.22} \end{align} \end{split}\]
\[\begin{split} \begin{align} \begin{aligned} \log L &= \log p(x_1, \cdots, x_N;\mu) \\ &= \sum_{i=1}^N \big\{ {x_i} \log\mu + (1-x_i)\log(1 – \mu) \big\} \\ &= \sum_{i=1}^N {x_i} \log\mu + \left( N-\sum_{i=1}^N x_i \right) \log( 1 – \mu ) \\ \end{aligned} \tag{9.2.28} \end{align} \end{split}\]
카테고리분포의 최대가능도 모수 추정¶
모수가 \(\mu = (\mu_1, \cdots, \mu_K)\)인 카테고리분포의 확률질량함수는 다음과 같다.
\[ \begin{align} p(x ; \mu_1, \cdots, \mu_K ) = \text{Cat}(x ; \mu_1, \cdots, \mu_K) = \prod_{k=1}^K \mu_k^{x_k} \tag{9.2.36} \end{align} \]
\[ \begin{align} \sum_{k=1}^K \mu_k = 1 \tag{9.2.37} \end{align} \]
이 식에서 \(x\)는 모두 \(k\)개의 원소를 가지는 원핫인코딩(one-hot-encoding)벡터다. 그런데 \(N\) 번의 반복 시행으로 표본 데이터가 \(x_1, \cdots, x_N\)이 있는 경우에는 모두 독립이므로 전체 확률밀도함수는 각각의 확률질량함수의 곱과 같다.
\[ \begin{align} L(\mu_1, \cdots, \mu_K ; x_1,\cdots, x_N) = \prod_{i=1}^N \prod_{k=1}^K \mu_k^{x_{i,k}} \tag{9.2.38} \end{align} \]
위 식에서 \(x_{i,k}\)는 \(i\)번째 시행 결과인 \(x_i\)의 \(k\)번째 원소를 뜻한다.
미분을 쉽게 하기 위해 로그 변환을 한 로그가능도를 구하면 다음과 같다.
\[\begin{split} \begin{align} \begin{aligned} \log L &= \log p(x_1, \cdots, x_N;\mu_1, \cdots, \mu_K) \\ &= \sum_{i=1}^N \sum_{k=1}^K \left( {x_{i,k}} \log\mu_k \right) \\ &= \sum_{k=1}^K \sum_{i=1}^N \left( \log\mu_k \cdot {x_{i,k}}\right) \\ &= \sum_{k=1}^K \left( \log\mu_k \left( \sum_{i=1}^N {x_{i,k}} \right) \right) \end{aligned} \tag{9.2.39} \end{align} \end{split}\]
\(k\)번째 원소가 나온 횟수를 \(N_k\)라고 표기하자.
\[ \begin{align} N_k = \sum_{i=1}^N {x_{i,k}} \tag{9.2.40} \end{align} \]
그러면 로그가능도가 다음과 같아지며 이 함수를 최대화하는 모수의 값을 찾아야 한다.
\[ \begin{align} \begin{aligned} \log L &= \sum_{k=1}^K \left( \log\mu_k \cdot N_k \right) \end{aligned} \tag{9.2.41} \end{align} \]
그런데 모수는 다음과 같은 제한조건을 만족해야만 한다.
\[ \begin{align} \sum_{k=1}^K \mu_k = 1 \tag{9.2.37} \end{align} \]
따라서 라그랑주 승수법을 사용하여 로그가능도에 제한조건을 추가한 새로운 목적함수를 생각할 수 있다.
\[ \begin{align} J = \sum_{k=1}^K \log\mu_k N_k + \lambda \left(1- \sum_{k=1}^K \mu_k \right) \tag{9.2.43} \end{align} \]
이 목적함수를 모수로 미분한 값이 0이 되는 값을 구하면 된다.
\[\begin{split} \begin{align} \begin{aligned} \dfrac{\partial J}{\partial \mu_k} &= \dfrac{\partial}{\partial \mu_k} \left\{ \sum_{k=1}^K \log\mu_k N_k + \lambda \left(1- \sum_{k=1}^K \mu_k\right) \right\} = 0 \;\; (k=1, \cdots, K) \\ \dfrac{\partial J}{\partial \lambda} &= \dfrac{\partial}{\partial \lambda} \left\{ \sum_{k=1}^K \log\mu_k N_k + \lambda \left(1- \sum_{k=1}^K \mu_k \right) \right\} = 0 & \\ \end{aligned} \tag{9.2.44} \end{align} \end{split}\]
이를 풀면 다음과 같이 모수를 추정할 수 있다.
\[ \begin{align} \dfrac{N_1}{\mu_1} = \dfrac{N_2}{\mu_2} = \cdots = \dfrac{N_K}{\mu_K} = \lambda \tag{9.2.45} \end{align} \]
\[ \begin{align} N_k = \lambda \mu_k \tag{9.2.46} \end{align} \]
\[ \begin{align} \sum_{k=1}^K N_k = \lambda \sum_{k=1}^K \mu_k = \lambda = N \tag{9.2.47} \end{align} \]
\[ \begin{align} \mu_k = \dfrac{N_k}{N} \tag{9.2.48} \end{align} \]
결론은 다음과 같다.
Likelihood (‘가능도’ 혹은 ‘우도’)와 MLE (Maximum Likelihood Estimation)
Likelihood (‘가능도’ 혹은 ‘우도’)
Likelihood는 관측된 데이터 집합 $\mathcal{D}$를 기반으로 하는 모델의 매개변수 $\theta$에 대한 함수라고 표현할 수 있습니다. 이렇게만 들으면 잘 이해가 가지 않으니 조금 더 풀어서 설명해보면 가능도 함수는 분포나 모델에 대한 매개변수 $\theta$에 대해 관측된 데이터 샘플들이 얼마나 그렇게 나타날 가능성이 있는지를 표현하는 함수입니다.
이래도 어려울 수 있어 또 다른 식으로 표현하면 어떤 사건 혹은 현상이 존재하고 어떤 분포에서 어느 정도의 확률인지를 보는 것입니다. 물론 여기서의 분포는 모델이 될 수도 있습니다.
위에서 설명한 딱딱한 정의를 내렸는데 이것만으로는 이해하기 난해할 것입니다.
이에 식과 함께 풀어서 설명해보도록 하겠습니다.
likelihood의 기본 전제는 관측된 데이터 샘플 혹은 관측된 무엇인가가 존재한다는 것입니다. 저는 여기서 다수의 $x_i$로 구성된 $\mathcal{D}$ 데이터 샘플 집합이 존재한다고 표기해보겠습니다.
$$\mathcal{D}= \{ x_1,\ x_2,\ \ldots , x_N \}$$
이 그림에서 데이터 샘플은 x=17, 20, 23를 $\mathcal{D}$로 표기할 수 있습니다.
여기에서 모델 혹은 분포가 존재하고 그 모델이나 분포를 설명하기 위한 매개변수가 존재합니다. 저는 여기서 이 매개변수를 $\theta$라 적겠습니다. 여기서 생각을 잘 하셔야하는 것이 우리는 매개변수 $\theta$를 적었지만 결국 이 $\theta$가 궁극적으로 의미하는 것은 이 $\theta$를 활용하여 구성된 모델 혹은 분포라는 것입니다.
가령 위 그림에서는 정규분포(Normal/Gaussian Distribution) 3개가 그려져 있는데 이 때 사용하는 파라미터 $\theta$는 각 정규분포별 $\mu , \sigma$를 의미할 것이고 이것이 파라미터 $\theta$가 될 것입니다. 만약 이것이 회귀 모델이라면 회귀 모델에 맞는 $y=ax+b$ 중 $a$와 $b$를 의미할 것입니다. 딥러닝의 구조 모델이라면 각 layer별 weight를 의미하는 $w$가 $\theta$를 의미할 것입니다.
여기까지 따라오셨다면 이제 가능도를 표기해보고 해석해보겠습니다.
맨 위에서 우리는 가능도를 관측된 데이터 집합 $\mathcal{D}$를 기반으로 하는 모델의 매개변수 $\theta$에 대한 함수라고 설명했습니다. 이를 그대로 식으로 풀어 쓰면 다음과 같습니다.
$$ \mathcal{L} (\theta ) = \mathcal{L} (\theta | \mathcal{D}) = p(\mathcal{D} | \theta )$$
만약 데이터가 i.i.d (identically independent distribution)이라면 각 데이터별로 얻은 확률의 곱으로 likelihood를 정의할 수 있습니다.
$$\mathcal{L} (\theta | \mathcal{D}) = p(\mathcal{D} | \theta ) = \prod_{i=1}^n p(x_i | \theta )$$
위 그림으로 따지면 빨간색 정규 분포에 대해 x=17, 20, 23에 대한 확률을 구해 각각 곱한 것을 의미합니다.
$$p(x_i | \theta ) = \frac{1}{ \sqrt{2\pi \sigma_{red}^2} } exp \{- \frac{(x_i – \mu_{red})^2}{2 \sigma_{red}^2} \} $$
물론 주어진 $\theta$인 $\mu , \sigma$가 녹색 정규 분포를 의미하면 그것에 대한 각각의 곱을 하고 황색에 대해서도 마찬가지입니다.
여기서 구한 likelihood를 잠깐 비교해보았을 때 $\mathcal{L} (\theta_{red}) < \mathcal{L} (\theta_{green})$이라면 녹색에 해당하는 likelihood가 빨간색에 비해 더 모수에 가깝다는 것을 의미합니다. 이것이 가능도입니다. 물론 Likelihood는 $\theta$에 대한 확률 분포가 아니기 때문에 모든 가능도의 합이 1이 되지 않을 수도 있습니다. MLE (Maximum Likelihood Estimation) 최대 가능도 추정 우리는 앞서 likelihood가 파라미터 $\theta$에 대해 특정 모델이나 분포의 value 값을 찾았고 이를 통한 가능도를 확인했습니다. 그런데 잘 생각해보면 가능도 중에서도 높은 가능도가 있는 것이 있을 것이고 우리가 제공한 데이터 샘플에 가장 잘 맞는 모델이나 분포의 파라미터 $\theta$가 존재할 것으로 예상됩니다. 여기서 우리는 likelihood를 maximum할 수 있는 estimation 즉, MLE를 진행하고 싶은 것입니다. 다시 말하면 최적의 파라미터 $\theta$를 찾고싶은 것입니다. MLE : 주어진 데이터를 제일 잘 설명하는 모델을 찾기 $$\hat{\theta} = argmax_{\theta } \mathcal{L} (\theta | \mathcal{D}) = argmax_{\theta } \prod_{i=1}^n p(\mathcal{D} | \theta )$$ 이때 계산의 편의성을 위해 log를 취함으로써 log likelihood를 구성하여 MLE를 진행합니다. Log Likelihood $$ln \mathcal{L} (\theta) = ln \mathcal{L} (\theta | \mathcal{D}) = \sum_{i=1}^n ln p(\mathcal{D} | \theta )$$ MLE with Log Likelihood $$argmax_{\theta } ln \mathcal{L} (\theta) = argmax_{\theta } ln \mathcal{L} (\theta | \mathcal{D}) = argmax_{\theta } \sum_{i=1}^n ln p(\mathcal{D} | \theta )$$ MLE with Gaussian distribution 가령 가우시안에 대한 파라미터 $\theta$ $\mu , \sigma$를 활용하는 분포를 likelihood라고 가정하면 다음과 같은 log likelihood를 적을 수 있습니다. $$ln p (x | \mu , \sigma^2) = - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 - \frac{n}{2} ln \sigma^2 - \frac{n}{2} ln (2 \pi )$$ 이를 이제 $\mu , \sigma$에 대한 미분을 진행하여 MLE를 구합니다. 기본적으로 미분으로 최대값을 구할 수 있기 때문입니다. $$\mu_{ML}$$ $$ {\partial ln p (x | \mu , \sigma^2) \over \partial \mu} = \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \mu_{ML}) = 0 $$ $$\sum_{i=1}^n x_i = n\mu_{ML}$$ $$\mu_{ML} = {1 \over n} \sum_{i=1}^n x_i$$ $$\sigma_{ML}^2$$ $${\partial ln p (x | \mu , \sigma^2) \over \partial \sigma} = {1 \over \sigma^3}\sum_{i=1}^n (x_i - \mu_{ML})^2 - \frac{n}{\sigma}=0 $$ $$\sigma_{ML}^2 = {1 \over n} \sum_{i=1}^n (x_i - \mu_{ML})^2$$ MLE with Bernoulli distribution 가령 예를들어 동전 던지기와 같은 독립 시행이 보장되는 Bernoulli distribution에서의 MLE는 다음과 같이 정의될 것입니다. $$\hat{\theta} = argmax_{\theta } \mathcal{L} (\theta | \mathcal{D}) = argmax_{\theta } \prod_{i=1}^n P(\mathcal{D} | \theta ) $$ $$= \prod_{i=1}^n p(x_i | p ) = _{n}\mathrm{C}_{m} p^m (1-p)^{(n-m)}$$ Log likelihood $$ln P (x | p) = _{n}\mathrm{C}_{m} (m ln p + (n-m) ln (1-p)) $$ $${\partial ln P (x | p) \over p } = _{n}\mathrm{C}_{m} m {1 \over p} - _{n}\mathrm{C}_{m} (n-m) {1 \over 1-p} = 0$$ $$p = {m \over n}$$ 번외) 딥 러닝 신경망 구조에서의 Likelihood와 MLE 만약 $y$ 정답이 존재하는 데이터 샘플이 주어졌을 때 신경망 모델의 가능도는 어떻게 표기할까요 $$x = \{ x_1,\ x_2,\ \ldots , x_N \} ,\ y = \{ y_1 ,\ y_2 ,\ \ldots ,\ y_N \}$$ $$\mathcal{D}= \{ (x1,y1),\ (x2,y2),\ \ldots ,\ (x_N, y_N) \}$$ $$ \mathcal{L} (\theta ) = \mathcal{L} (\theta | \mathcal{D}) = p(y|f_\theta (x)) $$ $f_\theta$ : $\theta$를 파라미터로 가지는 모델 혹은 분포 함수의 출력값 이때의 Likelihood 해석은 파라미터 $\theta$를 가지는 신경망에서의 예측값 혹은 출력이 나올 확률입니다. 이를 MLE 관점에서 확장해서 해석하면 네트워크의 출력값 ($f_\theta$)이 있을 때 우리가 원하는 정답 $y$가 높기를 바란다입니다. $$\hat{\theta} = argmin_{\theta } [- log(p(y|f_\theta (x))]$$ 주어진 데이터를 제일 잘 설명하는 모델을 찾기 -> 모델에 맞는 파라미터 $\theta$를 찾기가 되는 것입니다.
1) Gaussian
여기서 한 단계 더 나아가서 Gaussian distribution을 기반으로 보면 likelihood는 다음과 같습니다.
$$p(y_i | \mu_i, \sigma_i) = \frac{1}{ \sqrt{2\pi \sigma_{i}^2} } exp [- \frac{(y_i – \mu_{i})^2}{2 \sigma_{i}^2} ]$$
Log likelihood
$$ln p(y_i | \mu_i, \sigma_i) = ln \frac{1}{ \sqrt{2\pi \sigma_{i}^2} } – \frac{(y_i – \mu_i)^2}{2\sigma^2} $$
여기서 $\sigma =1$이라 가정하면
$$-ln p(y_i | \mu_i) \propto \frac{(y_i – \mu_i)^2}{2} $$
와 같이 표현이 가능합니다.
잘 보시면 Mean Square Error의 구조를 많이 닮아 있습니다.
다시 설명하면 log likelihood를 Gaussian으로 해석해서 MLE를 하면 MSE를 minimize하는 것과 같은 말이 된다는 것을 의미합니다.
역으로 생각하면 우리가 출력하고자 하는 $y$가 Gaussian distribution을 따른다면 MSE를 쓰는 것이 맞다고 해석할 수 있습니다. 그 때문에 continuous value에서는 MSE를 쓰는 것입니다.
2) Bernoulli
Bernoulli 역시 마찬가지입니다.
$$p (y_i | p_i) = p_i^{y_i} (1-p_i)^{1-y_i}$$
$$ln p (y_i | p_i) = y_i ln p_i + (1-y_i) ln (1-p_i)$$
$$-ln p (y_i | p_i) = -[y_i ln p_i + (1-y_i) ln (1-p_i)]$$
이 역시 Cross entropy를 닮아 있습니다.
즉, 다시 설명하면 log likelihood를 Bernoulli로 해석해서 MLE를 하면 Cross entropy를 minimize하는 것과 같은 말이 된다는 것을 의미합니다.
역으로 생각하면 우리가 출력하고자 하는 $y$가 Bernoulli distribution을 따른다면 Cross entropy를 쓰는 것이 맞다고 해석할 수 있습니다. 그 때문에 discrete value에서는 Cross entropy를 쓰는 것입니다.
Multinoulli에 대해서는 softmax를 쓰는 것입니다.
Reference
https://hyeongminlee.github.io/post/bnn001_bayes_rule/
https://hyeongminlee.github.io/post/bnn002_mle_map/
https://stats.stackexchange.com/questions/2641/what-is-the-difference-between-likelihood-and-probability
https://blog.naver.com/ivivaldi/221947736910
https://angeloyeo.github.io/2020/07/17/MLE.html
https://en.wikipedia.org/wiki/Likelihood_function#Background_and_interpretation
https://rpubs.com/Statdoc/204928
0000
위키백과, 우리 모두의 백과사전
최대가능도방법 (最大可能度方法, 영어: maximum likelihood method) 또는 최대우도법(最大尤度法)은 어떤 확률변수에서 표집한 값들을 토대로 그 확률변수의 모수를 구하는 방법이다. 어떤 모수가 주어졌을 때, 원하는 값들이 나올 가능도를 최대로 만드는 모수를 선택하는 방법이다. 점추정 방식에 속한다.
방법 [ 편집 ]
어떤 모수 θ {\displaystyle \theta } 로 결정되는 확률변수들의 모임 D θ = ( X 1 , X 2 , ⋯ , X n ) {\displaystyle D_{\theta }=(X_{1},X_{2},\cdots ,X_{n})} 이 있고, D θ {\displaystyle D_{\theta }} 의 확률 밀도 함수나 확률 질량 함수가 f {\displaystyle f} 이고, 그 확률변수들에서 각각 값 x 1 , x 2 , ⋯ , x n {\displaystyle x_{1},x_{2},\cdots ,x_{n}} 을 얻었을 경우, 가능도 L ( θ ) {\displaystyle {\mathcal {L}}(\theta )} 는 다음과 같다.
L ( θ ) = f θ ( x 1 , x 2 , ⋯ , x n ) {\displaystyle {\mathcal {L}}(\theta )=f_{\theta }(x_{1},x_{2},\cdots ,x_{n})}
여기에서 가능도를 최대로 만드는 θ {\displaystyle \theta } 는
> θ ^ > = > argmax θ > L ( θ ) {\displaystyle {\widehat {\theta }}={\underset {\theta }{\operatorname {argmax} }}\ {\mathcal {L}}(\theta )}
가 된다.
이때 X 1 , X 2 , ⋯ , X n {\displaystyle X_{1},X_{2},\cdots ,X_{n}} 이 모두 독립적이고 같은 확률분포를 가지고 있다면, L {\displaystyle {\mathcal {L}}} 은 다음과 같이 표현이 가능하다.
L ( θ ) = > ∏ i > f θ ( x i ) {\displaystyle {\mathcal {L}}(\theta )=\prod _{i}f_{\theta }(x_{i})}
또한, 로그함수는 단조 증가하므로, L {\displaystyle {\mathcal {L}}} 에 로그를 씌운 값의 최댓값은 원래 값 > θ ^ > {\displaystyle {\widehat {\theta }}} 과 같고, 이 경우 계산이 비교적 간단해진다.
L ∗ ( θ ) = log L ( θ ) = > ∑ i > log f θ ( x i ) {\displaystyle {\mathcal {L}}^{*}(\theta )=\log {\mathcal {L}}(\theta )=\sum _{i}\log f_{\theta }(x_{i})}
예제: 가우스 분포 [ 편집 ]
평균 μ {\displaystyle \mu } 와 분산 σ 2 {\displaystyle \sigma ^{2}} 의 값을 모르는 정규분포에서 x 1 , x 2 , ⋯ , x n {\displaystyle x_{1},x_{2},\cdots ,x_{n}} 의 값을 표집하였을 때, 이 값들을 이용하여 원래 분포의 평균과 분산을 추측한다. 이 경우 구해야 하는 모수는 θ = ( μ , σ ) {\displaystyle \theta =(\mu ,\sigma )} 이다. 정규분포의 확률 밀도 함수가
f μ , σ ( x i ) = 1 > 2 π > σ exp ( − ( x i − μ ) 2 2 σ 2 ) {\displaystyle f_{\mu ,\sigma }(x_{i})={\frac {1}{{\sqrt {2\pi }}\sigma }}\exp({\frac {-(x_{i}-\mu )^{2}}{2\sigma ^{2}}})}
이고, x 1 , x 2 , ⋯ , x n {\displaystyle x_{1},x_{2},\cdots ,x_{n}} 가 모두 독립이므로
L ( θ ) = > ∏ i > f μ , σ ( x i ) = > ∏ i > 1 > 2 π > σ exp ( − ( x i − μ ) 2 2 σ 2 ) {\displaystyle {\mathcal {L}}(\theta )=\prod _{i}f_{\mu ,\sigma }(x_{i})=\prod _{i}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp({\frac {-(x_{i}-\mu )^{2}}{2\sigma ^{2}}})}
양변에 로그를 씌우면
L ∗ ( θ ) = − n 2 log 2 π − n log σ − 1 2 σ 2 > ∑ i > ( x i − μ ) 2 {\displaystyle {\mathcal {L}}^{*}(\theta )=-{\frac {n}{2}}\log {2\pi }-n\log \sigma -{\frac {1}{2\sigma ^{2}}}\sum _{i}{(x_{i}-\mu )^{2}}}
가 된다. 식의 값을 최대화하는 모수를 찾기 위해, 양변을 μ {\displaystyle \mu } 로 각각 편미분하여 0이 되는 값을 찾는다.
∂ ∂ μ L ∗ ( θ ) = 1 σ 2 > ∑ i > ( x i − μ ) {\displaystyle {\frac {\partial }{\partial \mu }}{\mathcal {L}}^{*}(\theta )={\frac {1}{\sigma ^{2}}}\sum _{i}(x_{i}-\mu )} = 1 σ 2 ( > ∑ i > x i − n μ ) {\displaystyle ={\frac {1}{\sigma ^{2}}}(\sum _{i}x_{i}-n\mu )}
따라서 이 식을 0으로 만드는 값은 > μ ^ > = ( > ∑ i > x i ) / n {\displaystyle {\widehat {\mu }}=(\sum _{i}x_{i})/n} 으로, 즉 표집한 값들의 평균이 된다. 마찬가지 방법으로 양변을 σ {\displaystyle \sigma } 로 편미분하면
∂ ∂ σ L ∗ ( θ ) = − n σ + 1 σ 3 > ∑ i > ( x i − μ ) 2 {\displaystyle {\frac {\partial }{\partial \sigma }}{\mathcal {L}}^{*}(\theta )=-{\frac {n}{\sigma }}+{\frac {1}{\sigma ^{3}}}\sum _{i}(x_{i}-\mu )^{2}}
따라서 이 식을 0으로 만드는 값은 다음과 같다.
σ 2 = > ∑ i > ( x i − μ ) 2 / n {\displaystyle \sigma ^{2}=\sum _{i}(x_{i}-\mu )^{2}/n}
참고 문헌 [ 편집 ]
Lehmann, E. L.; Casella, G. (1998). 《Theory of Point Estimation》 (영어) 2판. Springer. ISBN 0-387-98502-6 .
Shao, Jun (1998). 《Mathematical Statistics》 (영어). New York: Springer. ISBN 0-387-98674-X .
같이 보기 [ 편집 ]
Maximum Likelihood Estimation의 이해
반응형
최대가능도 추정의 정의
최대가능도추정, Maximum Likelihood Estimation 혹은 최대우도법이라고 불리우는 이 방법은 어떤 확률 변수가 있을 때 주어진 데이터를 토대로 그 확률 변수의 모수 혹은 System Identification 분야에서 시스템 파라미터를 구하는 방법이다.
최근에는 Unsupervised Learning 분야 중 하나인 Generative Model 분야에서도 활발히 사용되고 있다.
어떤 미지의 값 θ 혹은 시스템 파라미터가 있다고 할 때 이를 기반으로 나올 수 있는 데이터가 확률 분포를 보인다고 하자. 주어진(관측된) 데이터가 이런 확률 분포를 통해서 나온 값이라고 할 때 이 데이터를 통해 미지의 θ 혹은 시스템 파라미터를 추정하는 방법이다.
통계학에서 주로 많이 사용되며, System Identification 분야에서 모델을 추정할 때 그리고 Generative Model에서는 학습된 feature model을 이용하여 data를 생성하는데 사용된다.
우리가 알고자하는 모델의 시스템 파라미터의 벡터를 θ라고하고, 확률 변수 집합을 D_θ = {x_1, x_2, …, x_n}이라고 하자. D_θ의 확률 밀도 함수Probability Density Function, PDF를 f라고 하고 확률 변수들에서 각각의 값 즉, 실험을 통해 얻어진 데이터를 x_1, x_2, …, x_n이라고 하면 가능도 L(θ; x_1, x_2, …, x_n)는 다음과 같다
여기서 데이터 f(x_1, x_2, …, x_n; θ)는 아래와 같이 계산할 수 있다.
즉, 미지의 파라미터 θ로 인하여 x_1, x_2, …, x_n의 데이터가 나올 확률 분포는 파라미터 θ로 인해 각 x_i 값이 나올 확률 분포의 총곱과 같다. 데이터 x_i를 이용하여 미지의 파라미터 θ를 구하기 위해 가능도를 최대로 만드는 함수는 다음과 같다
위 식의 의미는 가능도 L의 값을 최대로 만들기 위한 θ를 추정한다라는 말이다. 가능도를 쉽게 계산하기 위해 양변에 로그를 취하면
이다. 로그함수는 단조증가하므로 L에 로그를 취한 값의 최대 값 역시 우리가 구하려는 θ의 값과 같다.
함수 f를 어떤 확률 밀도 함수로 정하느냐에 따라서 최대 가능도를 계산하는 수식이 정해진다. 예를 들어, 가우시안Gaussian 분포는 갖느냐 아니면 이항Binomial 분포 모델을 갖느냐, 베르누이Bernoulli 분포를 갖느냐 등이다.
Gaussian Distribution을 갖는 확률 밀도 함수의 최대가능도 추정
여기서는 함수 f를 평균μ와 분산 σ^2를 갖는 가우시안 분포 모델을 적용해 보도록 하자. 앞서 설명했던 샘플링 데이터 x_1, x_2, …, x_n에 대해 평균과 분산을 estimation한다. 이 경우 구해야 하는 시스템 파라터는 θ = (μ, σ^2) 이다.
정규 분의 확률 밀도 함수의 식은
이며, x_1, x_2, …, x_n는 모두 독립이므로
양변에 로그를 취하면,
가능도함수 L*를 최대화 하는 값을 얻기 위해 우리가 구하고자 하는 시스템 파라미터 θ = (μ, σ^2)에 대해 각각 편미분을 수행하자.
맨 오른쪽의 괄호 안의 값이 0이 되어야 하니 μ 값의 추정치는 다음과 같다.
마찬가지로 분산도 같은 방식으로 정리하면,
따라서 이 식을 만족하는 분산의 추정는 다음과 같다.
머신러닝에서의 확률 분포와 최대 가능도 추정
업데이트 예정
반응형
키워드에 대한 정보 maximum likelihood estimation 설명
다음은 Bing에서 maximum likelihood estimation 설명 주제에 대한 검색 결과입니다. 필요한 경우 더 읽을 수 있습니다.
이 기사는 인터넷의 다양한 출처에서 편집되었습니다. 이 기사가 유용했기를 바랍니다. 이 기사가 유용하다고 생각되면 공유하십시오. 매우 감사합니다!
사람들이 주제에 대해 자주 검색하는 키워드 최대우도법(Maximum Likelihood Estimation) 소개
- 통계학
- 공돌이
- 수학정리
- statistics
- MLE
- maximum
- likelihood
- estimation
최대우도법(Maximum #Likelihood #Estimation) #소개
YouTube에서 maximum likelihood estimation 설명 주제의 다른 동영상 보기
주제에 대한 기사를 시청해 주셔서 감사합니다 최대우도법(Maximum Likelihood Estimation) 소개 | maximum likelihood estimation 설명, 이 기사가 유용하다고 생각되면 공유하십시오, 매우 감사합니다.